平行四辺形の面積 (2辺と間の角度) ツイート 面積の計算 ・ 正三角形の面積 ・ 三角形の面積 (底辺と高さ) ・ 三角形の面積 (2辺と間の角度) ・ 三角形の面積 (1辺と両端の角度) ・ 三角形の面積 (3辺の長さ) ・ 正方形の面積平行四辺形、三角形、台 形、ひし形などの面積につ いて、既習の面積の求め方 に帰着させて考え、計算で 求めようとする。 既習の面積の求め方を 基に、平行四辺形、三角形、 台形、ひし形などの面積の 求め方を工夫して考え、公 式をつくり出している。本単元では,三角形や平行四辺形,ひし形及び台形の面積の求め方を既習の求積可能な図形の面積 の求め方を基に考えたり,説明したり,公式をつくり出したりすることや,その過程で筋道を立てて 考える力の育成を図ることがねらいとなる。 また,求積方法を類推的に考える力や多様な考え

平行四辺形の面積は 底辺 高さ かけ算の順序の昔話
平行四辺形 ひし形 面積
平行四辺形 ひし形 面積- 上の平行四辺形の面積は (上底+下底)× 高さ となります。 台形の面積はその半分となるので 台形の面積=(上底+下底)× 高さ÷ 2 となります。 ひし形の面積 ひし形は対角線が直角に交わることから、対角線の長さがわかっていれば面積を求めること5年算数面積 教え方のポイント ① 三角形 と 平行四辺形と台形・ひし形の面積 の求め方 ② 三角形 と 平行四辺形と台形・ひし形の面積 求め方の公式 ③ いろいろな三角形・四角形の面積の求め方 ④ 面積



中2数学 基本解説プリント12 平行四辺形3 長方形とひし形 問題 232
を通して,筋道を立てて考える力を育成するのに適した題材である。また,三角形,平行四辺形,台 形,ひし形と繰り返し既習の面積公式を活用することで,新たな課題を解決する態度も養うことがで きる。 これらのことから,本単元で既習の図形の求積方法を基に新たな図形の面積の求め方ひし形の面積=一方の対角線×もう一方の対角線÷2 取り組んだ日 月 日 この場合、ななめの辺 の長さは使いません。 底辺 高さ プリントを回転させよう。 が下です。 高さ 底辺 三角形は2つ合わせると 平行四辺形になります。 平行四辺形の半分だから 下底 上底と同じ 高さ 底辺 上底 ミズキ こんにちは、ミズキです。 ミズキ 今回は様々な四角形について、一緒に考えていきましょう。 カイト よろしくな! ミズキ! ミズキ アオイくんにも、手伝ってもらいます。 アオイ カイにも分かるように、頑張って教えよう。 ミズキ さて、それでは、まず平行四辺形の面積の公式に
各辺の長さ計算は不要です5年算数面積 教え方のポイント ① 三角形 と 平行四辺形と台形・ひし形の面積 の求め方 ② 三角形 と 平行四辺形と台形・ひし形の面積 求め方の公式 ③ いろいろな三角形・四角形の面積の求め方 ④ 面積と比例の こんにちは。所長@冬休み中です。 年も残りわずかですがいかがお過ごしでしょうか。 今日も指導のふりかえりをしてみます。 図形の面積単元は、平行四辺形、三角形、台形、ひし形の面積を求める学習です。これは私の観点ですが、いわゆる図形領域こそictの効果を発揮できるものイ 平行四辺形,三角形,台形,ひし形等の面積の求め方を,既習の求積方法に着目して,具体的に操 作して考えている。 思考力・判断力・表現力等 ウ 平行四辺形,三角形,台形,ひし形等について,具体的な操作を通して,既習の面積の求め方に関 連させて,それぞれの図形の捉え方を
5年生算数"面積" 小学校5年生 授業「算数」 採用1年目(194~3) この単元では、長方形と正方形の面積は求めることができる子ども達が、三角形、平行四辺形、そして台形、ひし形の面積の求め方を学習していきます。 面積の学習は、具体物を教材(ア) 三角形、平行四辺形、ひし形、台形の面積の計算による求め方 について理解すること。 ②未知の状況にも対応できる「思考力、判断力、表現力等」 (ア) 図形を構成する要素などに着目して、基本図形の面積の求め方を見 いだす とともに、その表現を振り返り、簡潔かつ的確な表現に高め平行四辺形からひし形までの面積を求める学習は,指導内容に継続性があり,子供 にとっては既習事項を生かしながら様々な求め方を考え出していくことができる教材 である。こうした学習を通して,面積を求める楽しさを味わうとともに筋道を立てて 考え,表現していく力を伸ばしていく



1




四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun
知識・技能 三角形,平行四辺形,台形,ひし形の面積の求め方について理解できる。 思考力・判断力・表現力等 図形を構成する要素などに着目して,面積の求め方を見いだすとともに,その 表現を振り返り,簡潔かつ的確な表現に高め,公式を導くことができる。 学びに向かう力,人間性 既ア 三角形、平行四辺形、ひし形及び台形の面積の求め方を考えること。 本単元では、等積変形や倍積変形を利用して、平行四辺形や三角形などの面積を多様な考え方で求め る活動を位置付ける。その活動を通して、既習の求積公式が利用できる図形に変形本単元の指導にあたっては,平行四辺形,三角形,台形,ひし形の面積を工夫して求める能力を伸 ばすとともに,簡潔かつ的確な表現へと高める能力を一層伸ばすことをねらいとしている。 単元の導入段階では,求積可能な形とそうでない形があることに気付かせ,本単元の見通しをもつ こと



平行四辺形とひし形って何がちがうんですか ひし形は対角線が垂 Yahoo 知恵袋




四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ
三角形・平行四辺形・ ひし形・台形の面積 年 組 名前 取り組んだ日 月 日 1 次の平行四辺形の面積を求めましょう。(ただし、1マスは1㎝の正方形です) ① 式 答え ② 式 答え 6 ㎝ 13 ㎝ 5 ㎝ 9 5年 (2) 三角形・平行四辺形・ ひし形・台形の面積 年 組 名前 取り組んだ日 月 日 1 次のア 三角形、平行四辺形、ひし形及び台形の面積の求め方を考えること。 児童は、これまでに第4学年で面積の共通単位や長方形や正方形の面積の求め方を学習し てきている。本単元では、三角形、平行四辺形、ひし形、台形などの面積の求め方を考える形,平行四辺形,台形,ひし形の面積の意味理解と,面積公式を導き出すことを行っていく。ここでは,単に 個々の図形の面積公式を記憶して,使用できるだけがねらいではない。重要なことは,図形の一部を分割したり, 「面積」 ・面積の概念と普遍単位(cm2,m2,km2
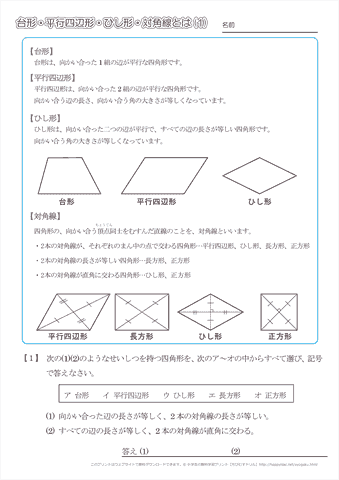



小学4年生の算数 台形 平行四辺形 ひし形 対角線 問題プリント ちびむすドリル 小学生



長方形への等積変形 面積 量計算 数学教育
目し、平行四辺形。 (以下省略) ②平行四辺形の面積の 公式を考え、それを適 して面積を求めよ うとしている。 (観察・ノート) 9 本 時 ひ ひし形の面積の求め方を 考え、説明する活動を通し、 ひし形の面積を求める公式 をつくり出すことができる。 平行四辺形の上に、(底辺)=2、(高さ)=3の長方形をのせました。 (両方の底辺を重ねています) みなさんは長方形の面積が(底面)×(高さ)で求められることはご存じだと思います。 なので、この長方形の面積が平行四辺形の面積に等しいことがわかれば、ア(ア) 三角形,平行四辺形,ひし形,台形の面積の計算による求め方について理 解すること。 イ(ア) 図形を構成する要素などに着目して,基本図形の面積の求め方を見いだす とともに,その表現を振り返り,簡潔かつ的確な表現に高め,公式として導 くこと。 第6学年 B(2
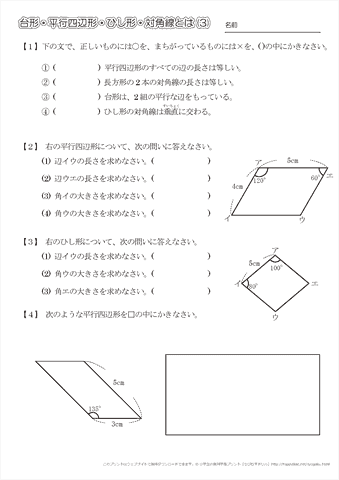



小学4年生の算数 台形 平行四辺形 ひし形 対角線 問題プリント ちびむすドリル 小学生




平行四辺形の辺や角を求める Youtube
台形,平行四辺形,ひし形の対角線の長さは等しいとは限りません.他は図のように等しくなります. →閉じる← 4. 対角線はそれぞれの頂角を2等分する.1組の等しい対辺の長さをa、他の辺をb、cとし、1組の等しい対角の大きさをθとしますと、余弦定理から、対角線について次の関係が得平行四辺形、三角形、台形、ひし形などの面積を公式を用 いて求めることができる。 知識・理解 平行四辺形、三角形、台形、ひし形などの計算による面積 の求め方を理解する。 関連と発展 4 年 垂直・平行と四角形 垂直・平行の定義、かき方 台形、平行ひし形の面積の求め方を考える。 ・ 三角形や長方形を基に、ひし形 の面積の求め方を説明する。 児童が説明する算数的活動⑥ ひし形を求積 できる図形に 変形し、進んで ひし形の面積 を求めようと している。(ア、 イ) ひし形の面積 の求め方をい ろいろ考え、説 明することが できる




5年算数 三角形の面積 指導の反省 ネコ好きな学校の先生の日常
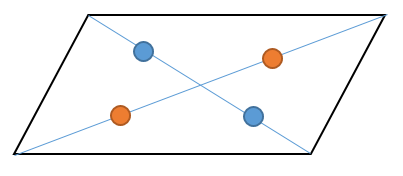



小学算数 平行四辺形 ひし形 長方形 正方形の対角線は真ん中で交わる 偏差値40プログラマー
・平行四辺形,三角形,台形,ひし形などの面積を公式を用いて求めることができる。 知識・理解 ・平行四辺形,三角形,台形,ひし形などの計算による面積の求め方を理解する。 4 指導計画(14時間) 小単元 時数 学習内容 1 平行四辺形の三角形、平行四辺形、台形、ひし形などの面積の求め方について、算数的活動を通して既習の面 積の求め方に帰着して考えようとしている。 算数への関心・意欲・態度 既習の面積の求め方をもとに、三角形や平行四辺形などの面積を工夫して求めることができる。 数学的な考え方ア 三角形,平行四辺形,ひし形及び台形の面積の求め方を考えること。 〔算数的活動〕(1) イ 三角形,平行四辺形,ひし形及び台形の面積の求め方を,具体物を用いたり,言葉, 数,式,図を用いたりして考え,説明する活動 平面図形の面積については,第4学年で長方形や正方形の面積の
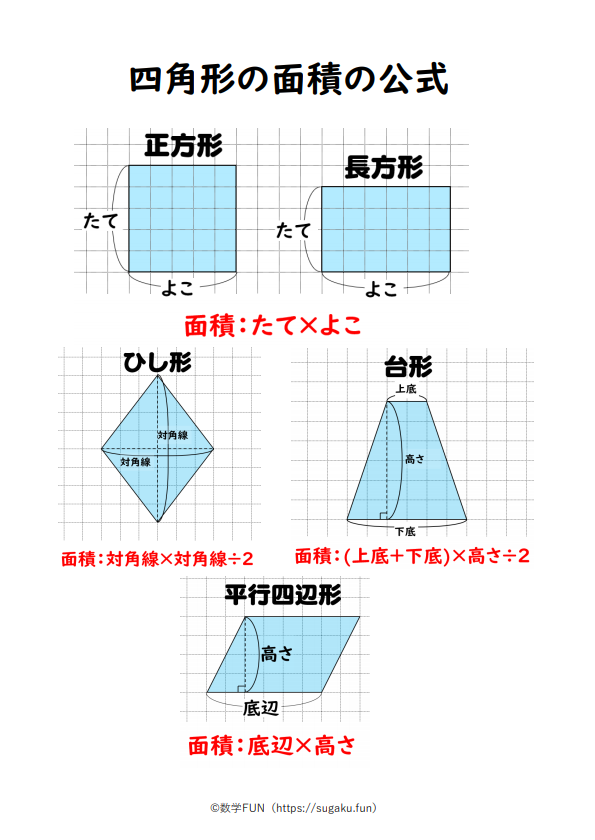



四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun




平行四辺形の面積は 底辺 高さ かけ算の順序の昔話
特に,相似な三角形の面積比は相似比の二乗に比例することも分かります。 →相似比と面積比,体積比の公式の証明 また,サインの性質: sin θ = sin (18 0 ∘ − θ) \sin \theta=\sin (180^{\circ}\theta) sin θ = sin (18 0 ∘ − θ) に注意すると,円に内接する四角形四角形の面積の求め方(公式) 三角形教科書 5年 unit 632 三角形と四角形の面積 平行四辺形、ひし形、台形の面積 例題と解説 トレーニング 確認テスト ログインが必要です フィードバック (不具合・誤記・問題解法の矛盾に関する連絡) ご利用頂きまして誠にありがとうございます。 ご記入




面積 上 面積の意味から 正方形 長方形 平行四辺形 三角形の面積の求 思考力算数練習張シリーズ 39 M Access 本 通販 Amazon
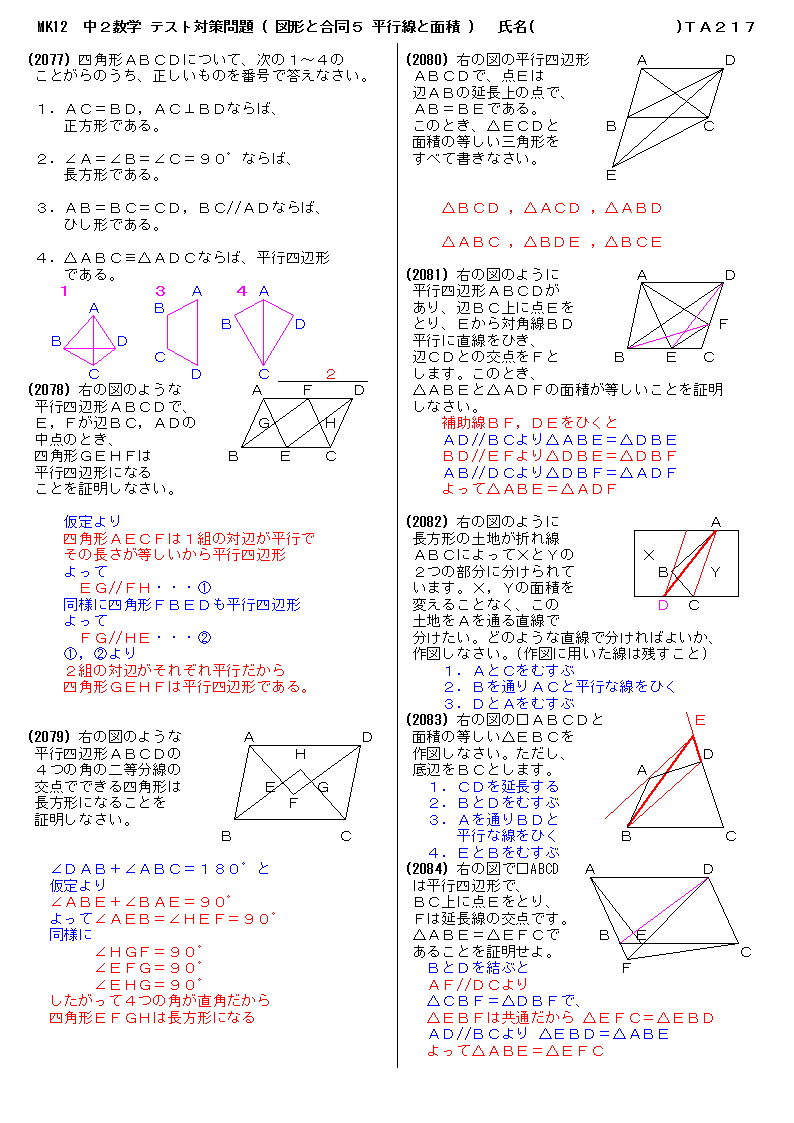



無料 中2数学 テスト対策 解答プリント 217 図形と合同5 平行線と面積




正方形 Wikipedia




ひし形の面積 練習 Youtube




簡単公式 ひし形 菱形 の面積を計算できる2つの求め方 Qikeru 学びを楽しくわかりやすく




中学受験算数 平行四辺形の面積を求める問題 Okwave




ボード 勉強 のピン
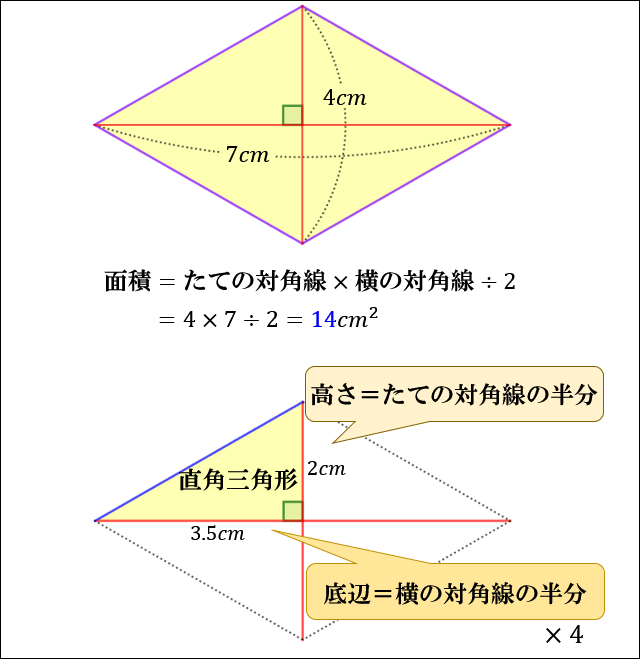



四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ
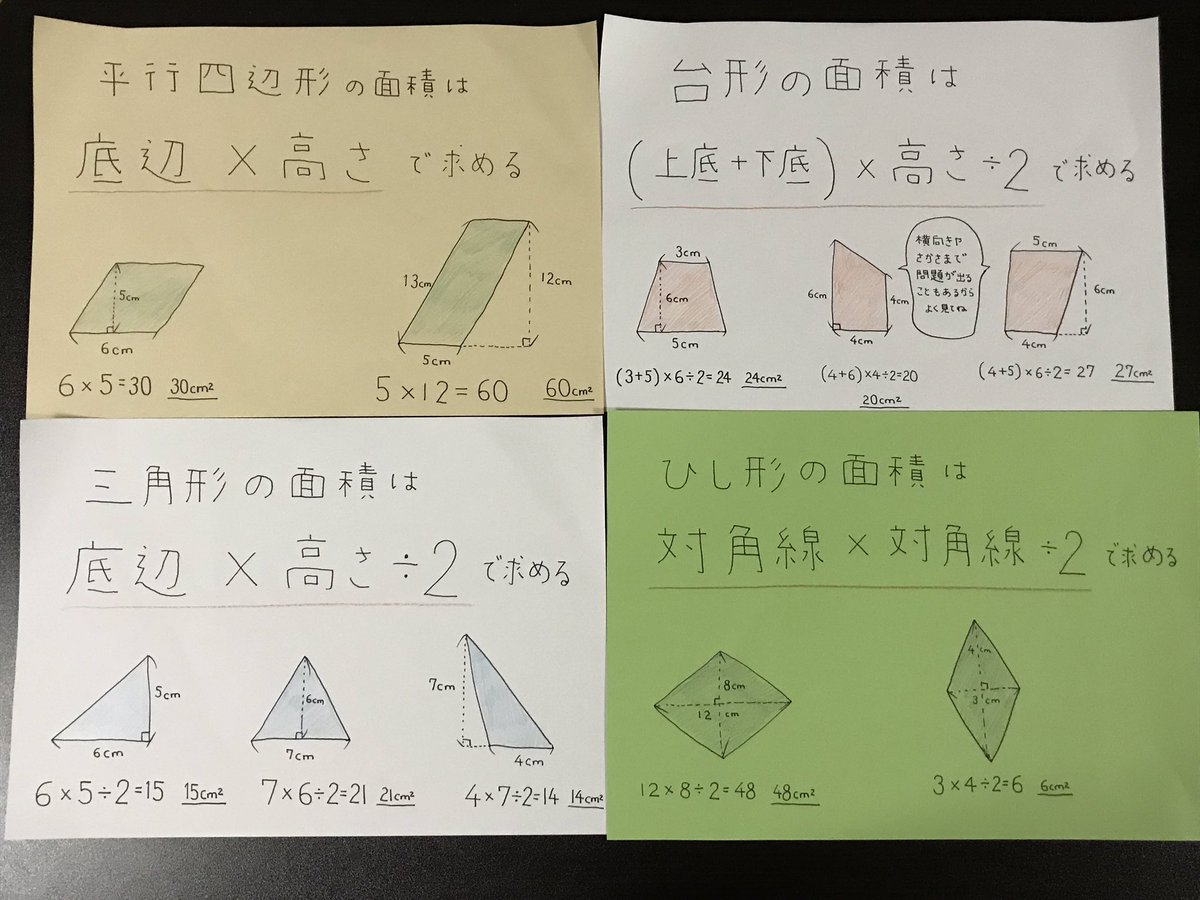



M A A 平行四辺形 三角形 台形 ひし形の面積を求める公式を画用紙にまとめた いま学校で習っている単元なので トイレに貼っておく 小5算数



中丹教育局
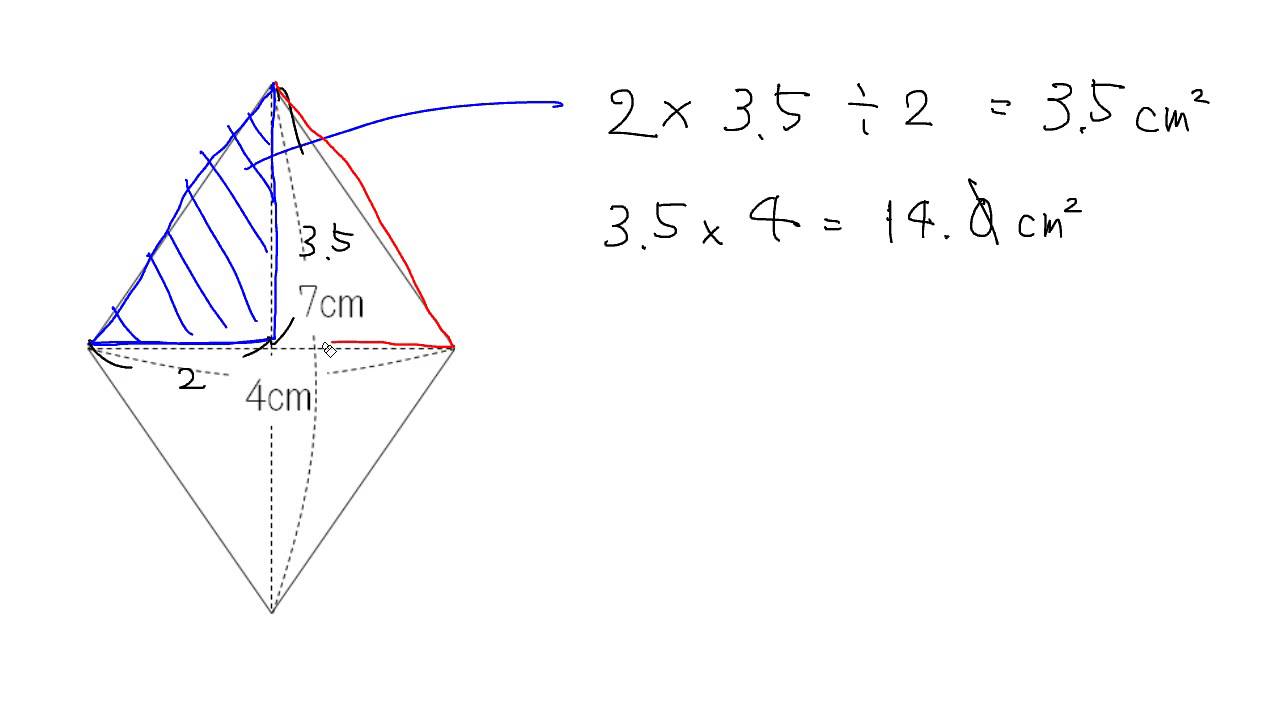



ひし形の面積の公式 Youtube
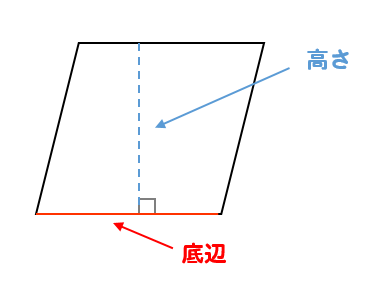



平行四辺形とひし形の違いってなに それぞれの特徴を比較 数スタ



中2数学 基本解説プリント12 平行四辺形3 長方形とひし形 問題 232
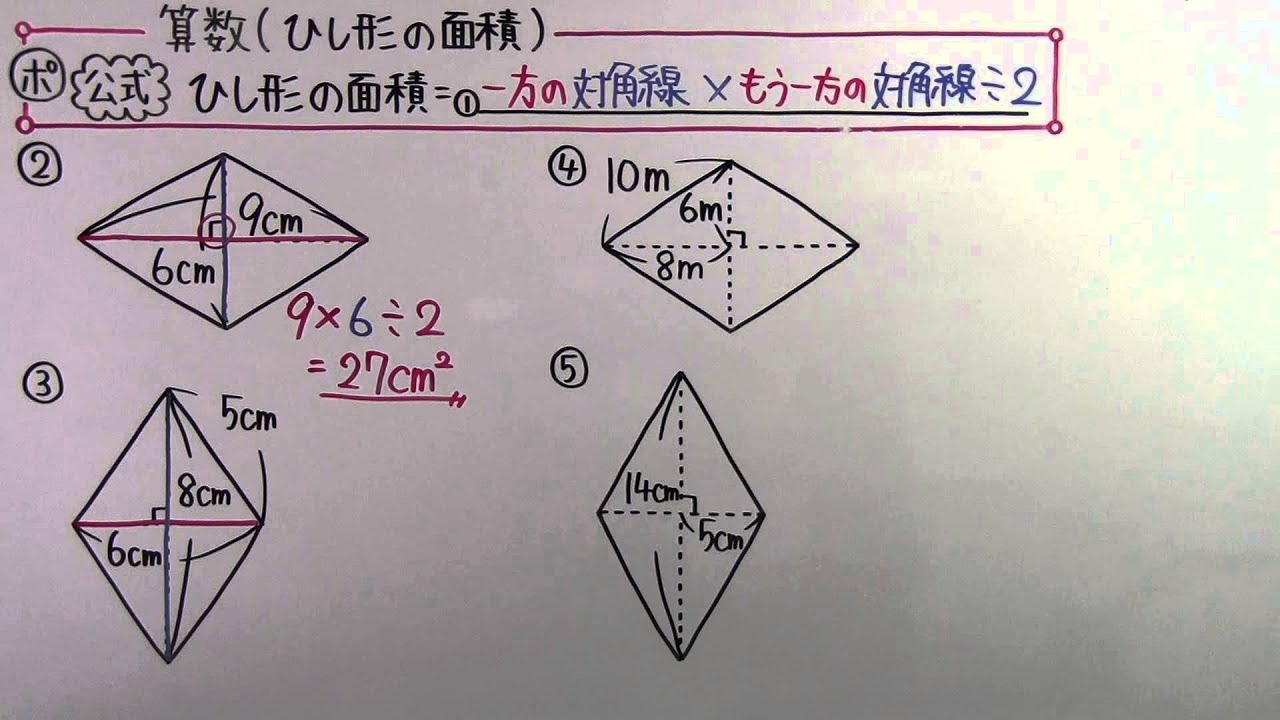



小5 算数 小5 44 ひし形の面積 Youtube




台形と平行四辺形を平行な辺の組の数で分類することは 原理的に不可能である 小学校4年生の算数 身勝手な主張




ひし形の面積の公式 面積の求め方は対角線に注目しよう 中学や高校の数学の計算問題



特別な平行四辺形2




勉強しよう数学 ひし形の対角線の直交の公式と2重平行四辺形の面積の公式
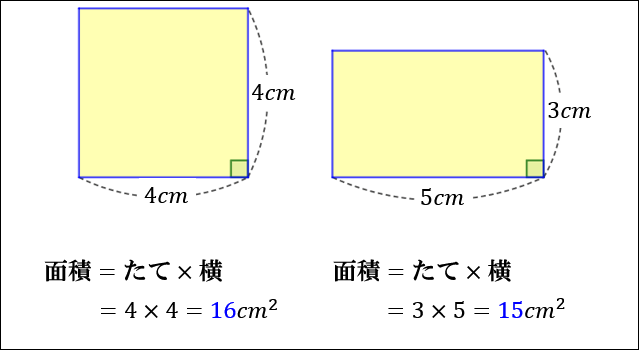



四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ




7 X 6cpi 7cn 4cn Square 2 Lihat Cara Penyelesaian Di Qanda




簡単公式 ひし形 菱形 の面積を計算できる2つの求め方 Qikeru 学びを楽しくわかりやすく




小学5年生 ひし形 台形の面積 算数 Active Learning 学院




5年算数面積 教え方のポイント
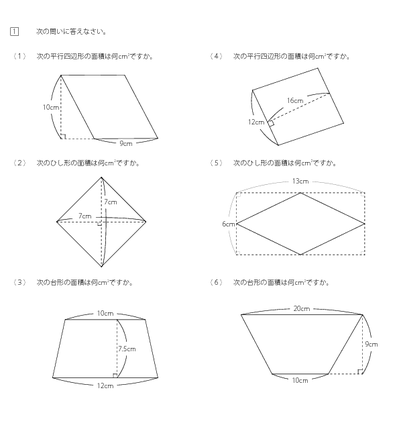



みんなの算数オンライン 教科書 平行四辺形 ひし形 台形の面積



長方形の計算 もう一度やり直しの算数 数学




算数 図形の面積2 平行四辺形 授業力アップ 学級経営の話
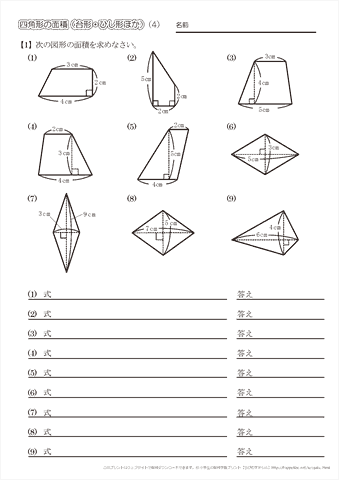



小学5年生の算数 四角形の面積 台形 ひし形ほか 問題プリント ちびむすドリル 小学生
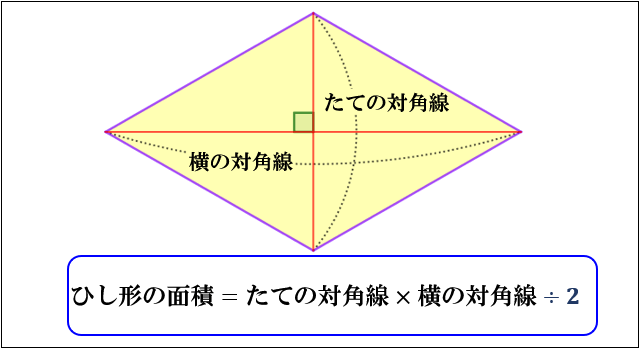



四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ
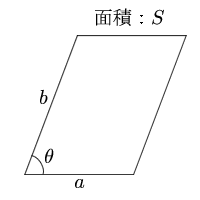



平行四辺形 2辺と間の角度 面積の計算 計算サイト



Www City Ota Tokyo Jp Kyouiku Topics Syougakuseigakusyu Files Gonensansuumondai Pdf




公式なんて覚えない ひし形の面積は直感的に考えよう
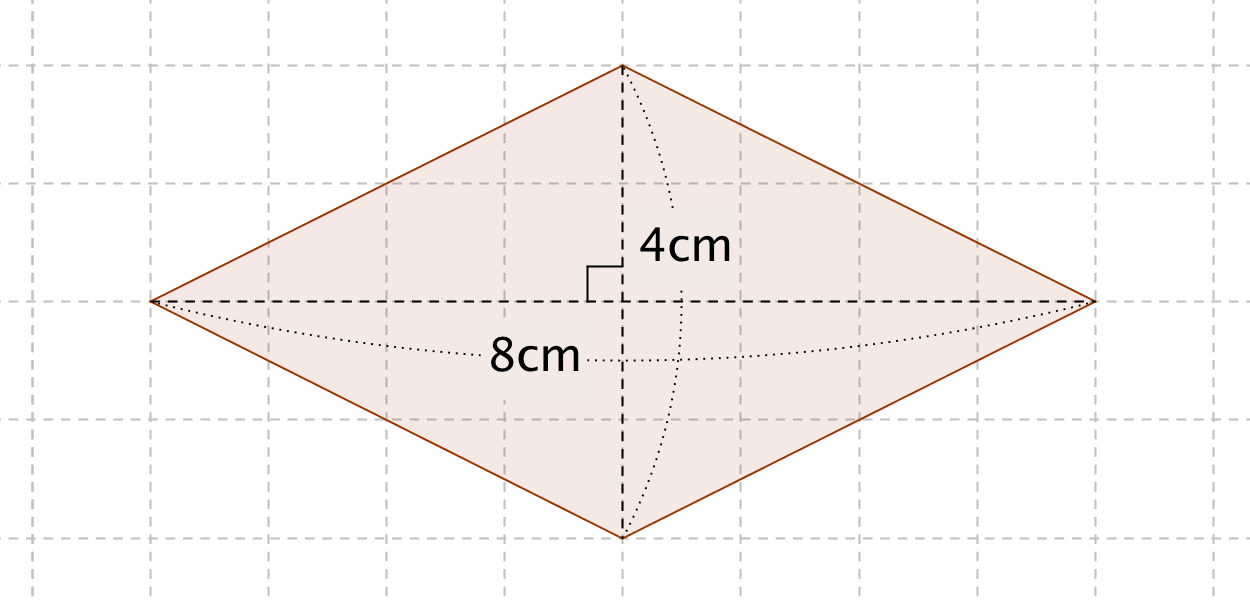



ひし形の面積の公式 算数の公式
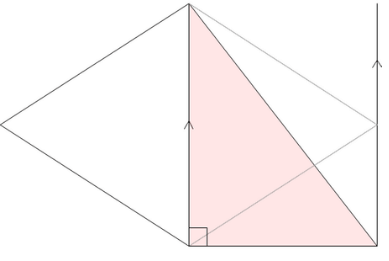



小学校で習うひし形の面積の求め方 対角線を使った公式で求められる理由 みけねこ小学校
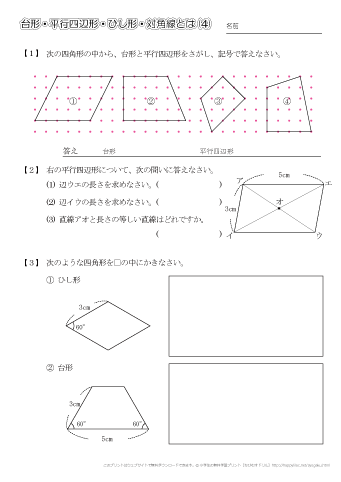



小学4年生の算数 台形 平行四辺形 ひし形 対角線 問題プリント ちびむすドリル 小学生
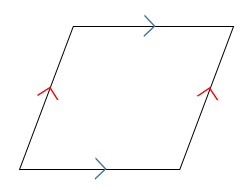



平行四辺形とひし形の違いってなに それぞれの特徴を比較 数スタ




公式なんて覚えない ひし形の面積は直感的に考えよう
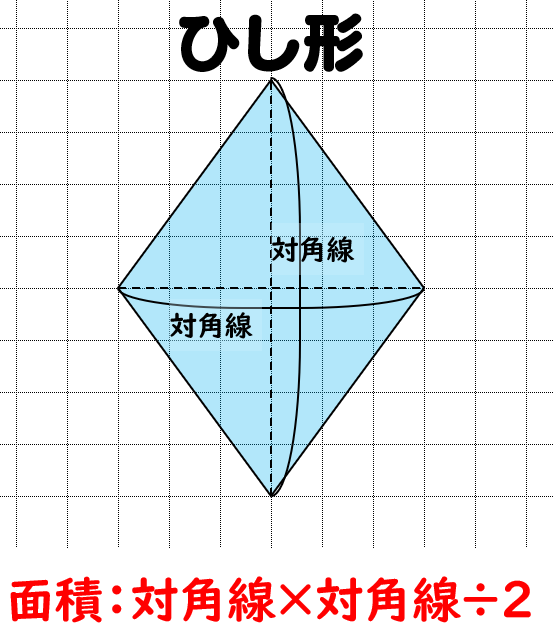



ひし形の面積の公式 小学生に教えるための分かりやすい解説 数学fun



1
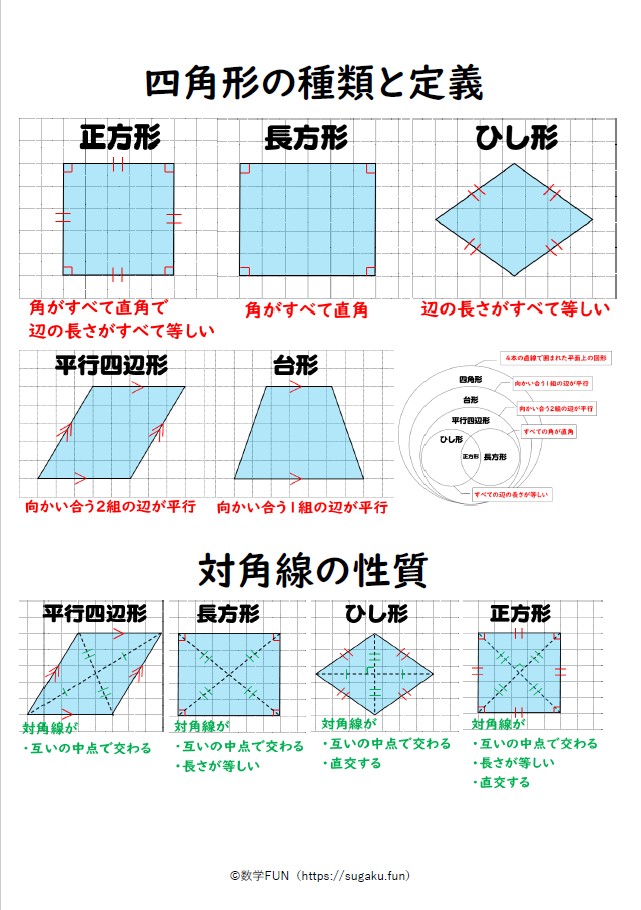



四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun




小学5年生の算数 四角形の面積 台形 ひし形ほか 問題プリント ちびむすドリル 小学生
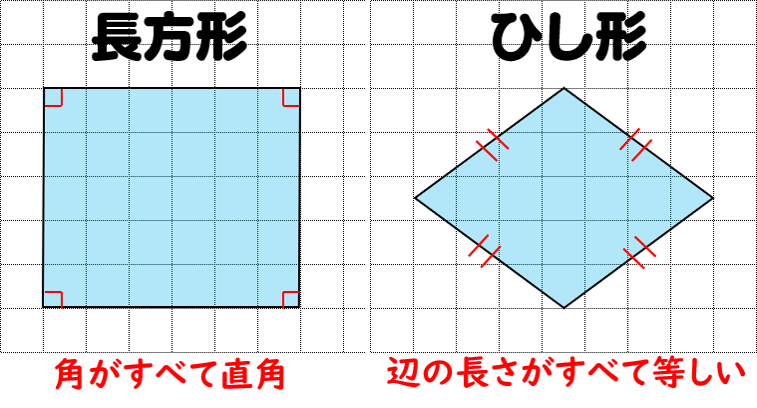



四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun



四角形の性質 ひし形の性質 平行四辺形の性質 正方形の性質 長方形の性質 女子学院中学 05年 平成17年度 入試算数問題 まいにち一題 中学受験過去問題研究
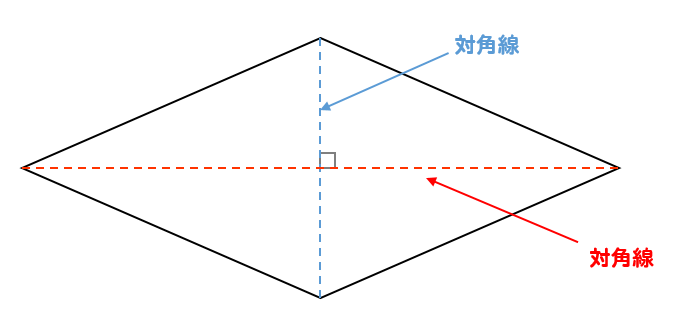



平行四辺形とひし形の違いってなに それぞれの特徴を比較 数スタ
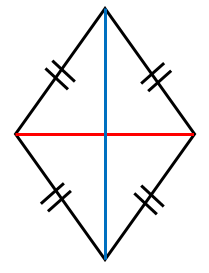



ひし形の面積を求める方法と例題 具体例で学ぶ数学




簡単公式 ひし形 菱形 の面積を計算できる2つの求め方 Qikeru 学びを楽しくわかりやすく
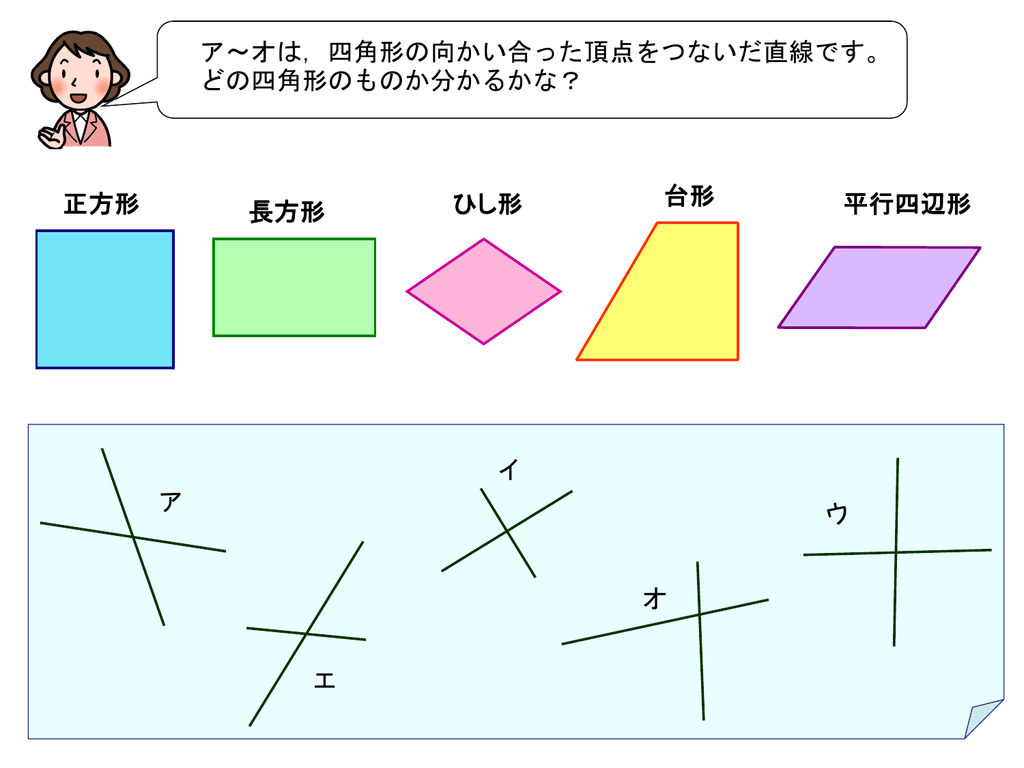



正方形 長方形 ひし形 台形 平行四辺形



教材総合カタログ 19 小学校全教科




小学生 平行四辺形と長方形のちがいは Active Learning 学院



ひし形 菱形 とは 定義や面積の求め方 公式 計算問題 受験辞典




平行四辺形の面積の求め方 公式と計算例



Http Cms Nerima Tky Ed Jp Weblog Files 142 Doc Pdf




四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun



Www Tsumugi Ne Jp Member Data Sm2 5 Sm2 5 4 Pdf



1
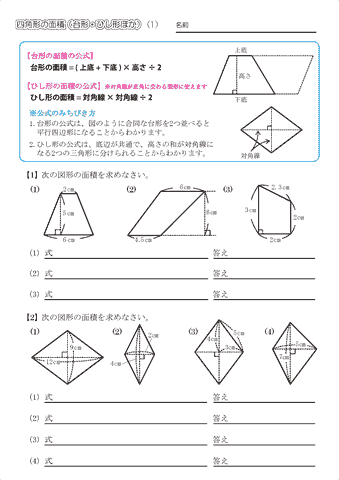



小学5年生の算数 四角形の面積 台形 ひし形ほか 問題プリント ちびむすドリル 小学生
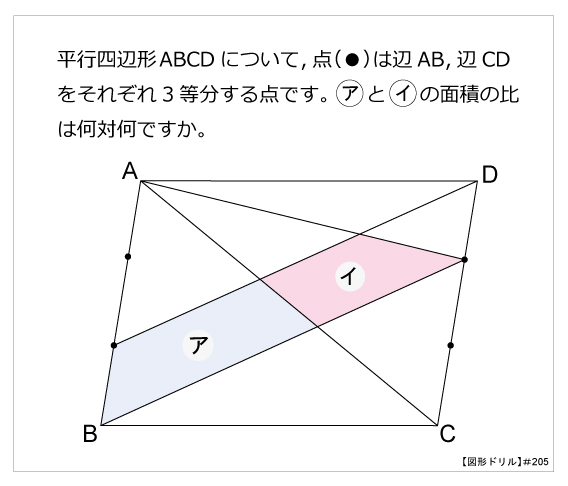



図形ドリル 第5問 平行四辺形内の面積比 算数星人のweb問題集 中学受験算数の問題に挑戦



2




高校数学b ベクトルの成分表示と平行四辺形 受験の月
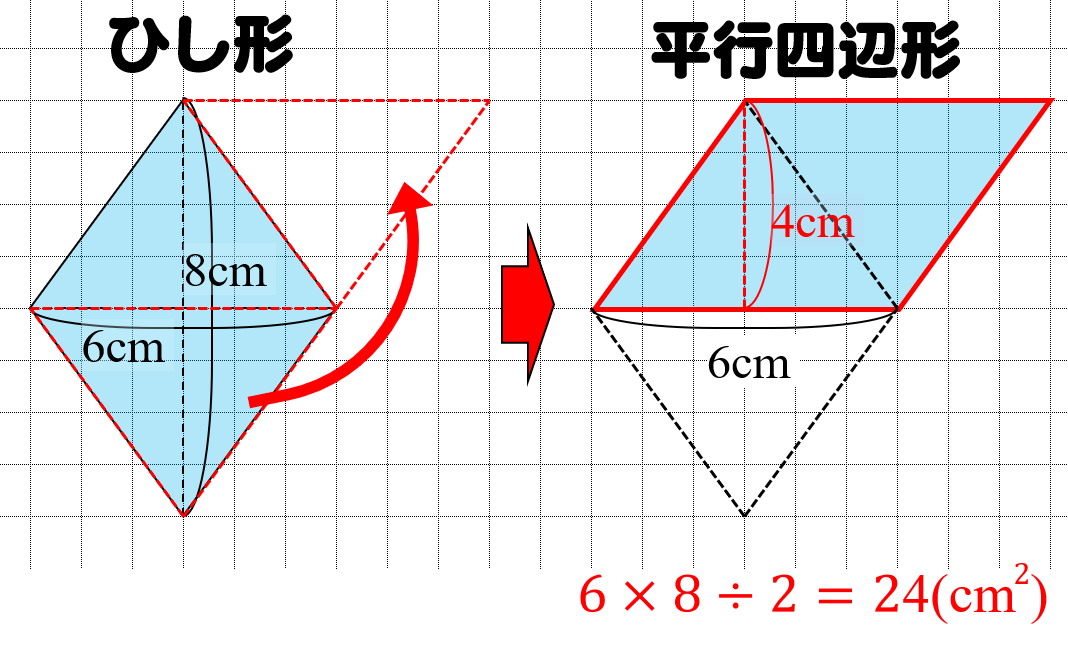



ひし形の面積の公式 小学生に教えるための分かりやすい解説 数学fun




平行四辺形とひし形の違いってなに それぞれの特徴を比較 数スタ



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典




ひし形の面積の公式 小学生に教えるための分かりやすい解説 数学fun




小学校6年生算数 平行四辺形の面積 再掲 13 12 30 に質問があり 数学 教えて Goo




平行四辺形の面積の求め方 公式と計算例




中2数学 長方形 ひし形 正方形 映像授業のtry It トライイット
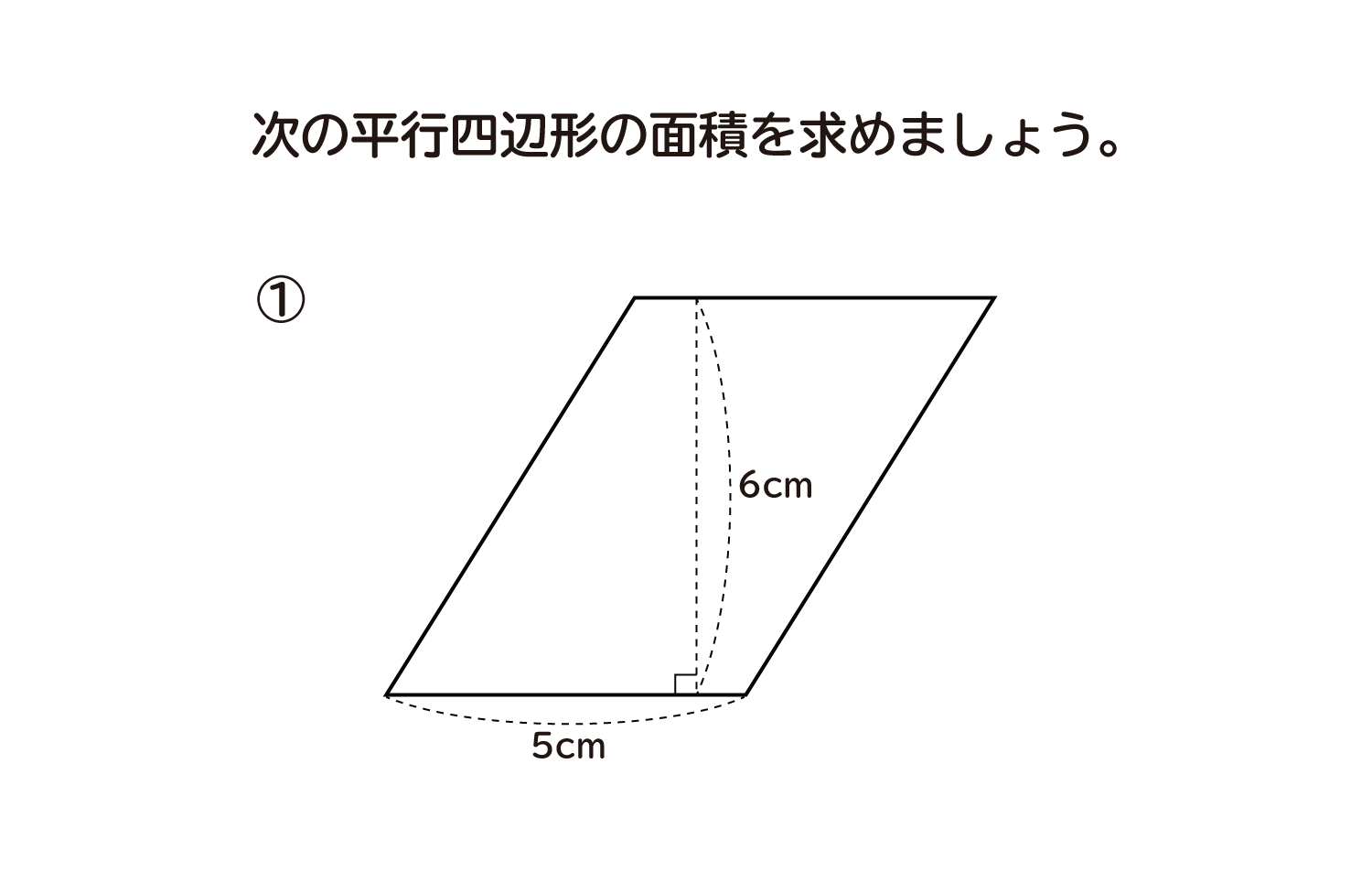



小学5年生 算数 無料問題集 平行四辺形の面積 おかわりドリル




5年算数面積 教え方のポイント




公式なんて覚えない ひし形の面積は直感的に考えよう
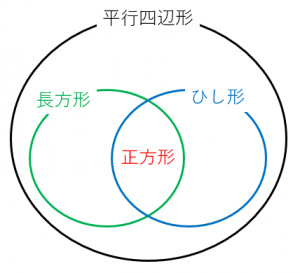



平行四辺形 ひし形 長方形 正方形の違い 具体例で学ぶ数学



教育ソフト開発研究所 5年5巻



ひし形の定義は 1分でわかる定義 正方形 平行四辺形との違い 対角線との関係



Http Www Ogaki City Ed Jp Open Education Scholarship Math Plan 5nen 11 Pdf
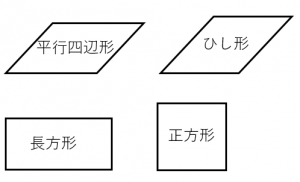



平行四辺形 ひし形 長方形 正方形の違い 具体例で学ぶ数学




すきるまドリル 小学5年生 算数 図形の面積 無料学習プリント すきるまドリル 無料学習プリント



みんなの算数オンライン 教科書レベル 5年 三角形と四角形の面積 平行四辺形 ひし形 台形の面積 例題と解説
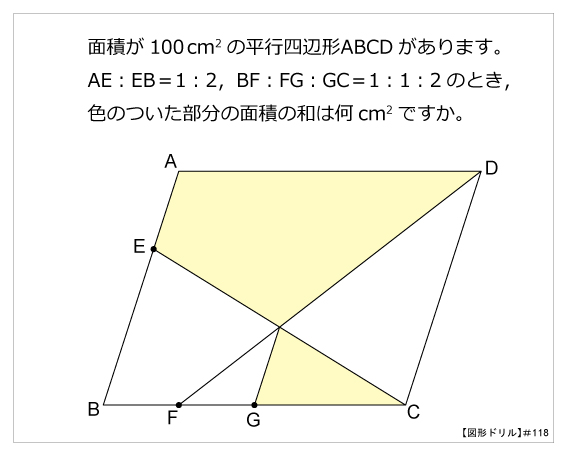



図形ドリル 第118問 平行四辺形の面積の和 算数星人のweb問題集 中学受験算数の問題に挑戦



ひし形の定義は 1分でわかる定義 正方形 平行四辺形との違い 対角線との関係
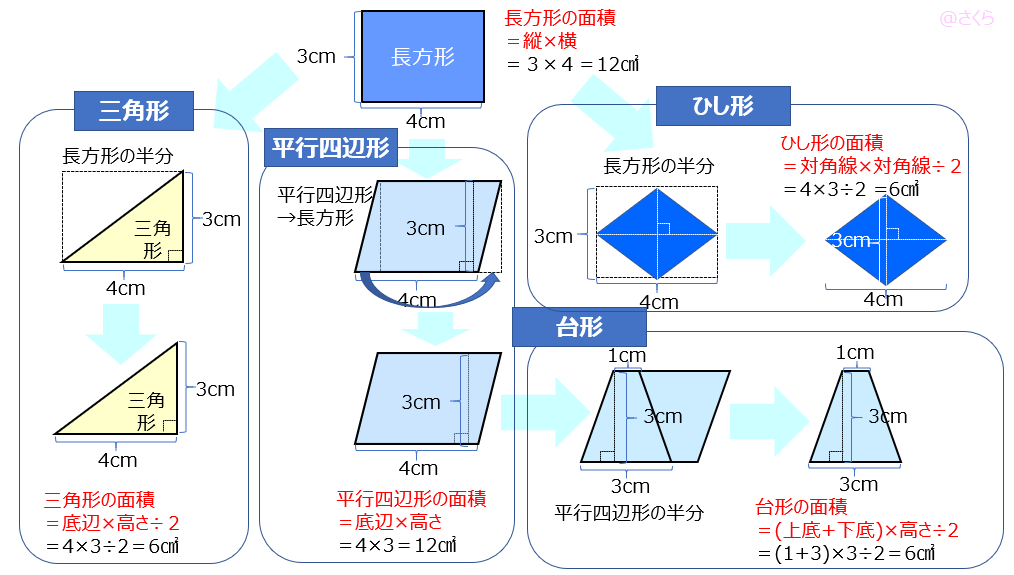



四角形の種類と性質 面積の公式について 中学受験 ゲーム大好き息子の偏差値32からの挑戦
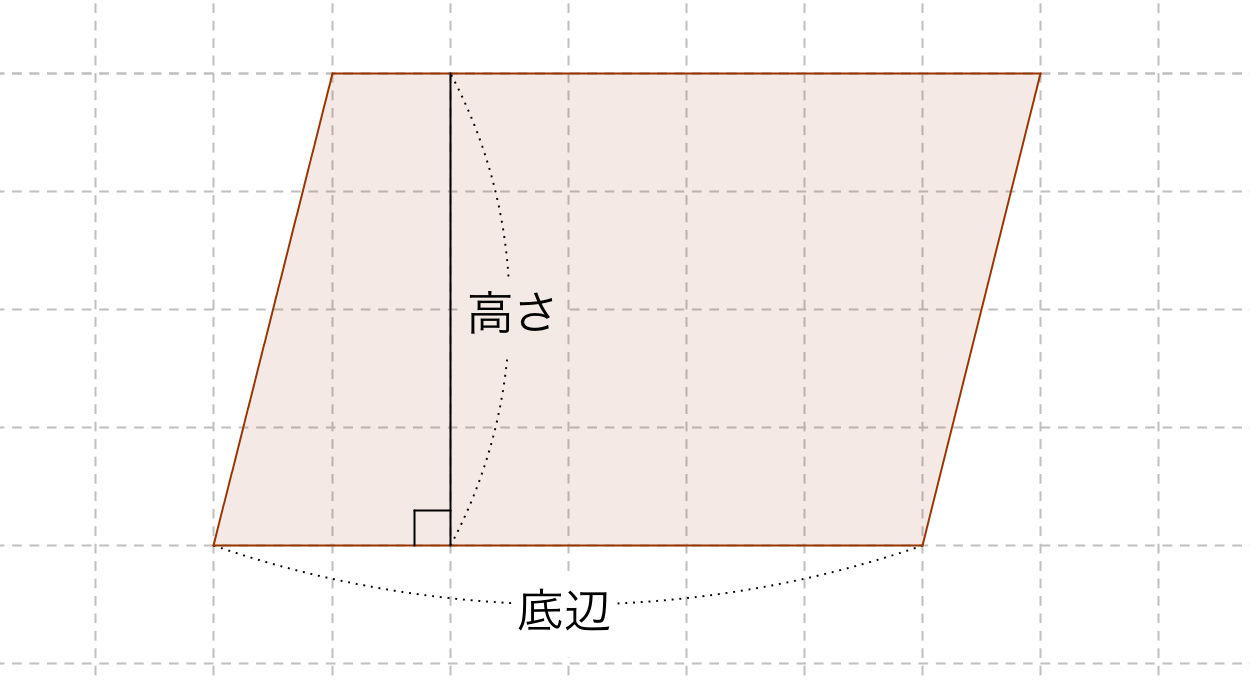



平行四辺形の面積の公式 算数の公式




無料の学習プリント 小学4年生の算数ドリル いろいろな四角形 みそにゃch




2 1の授業と 総復習 得点力 数学 受験ブログ




平行四辺形の面積の求め方 公式と計算例




6月4日 小4算数 ジャングルジムブログ




無料 中2数学 標準問題 解答プリント 232 平行四辺形3 長方形とひし形




簡単公式 ひし形 菱形 の面積を計算できる2つの求め方 Qikeru 学びを楽しくわかりやすく
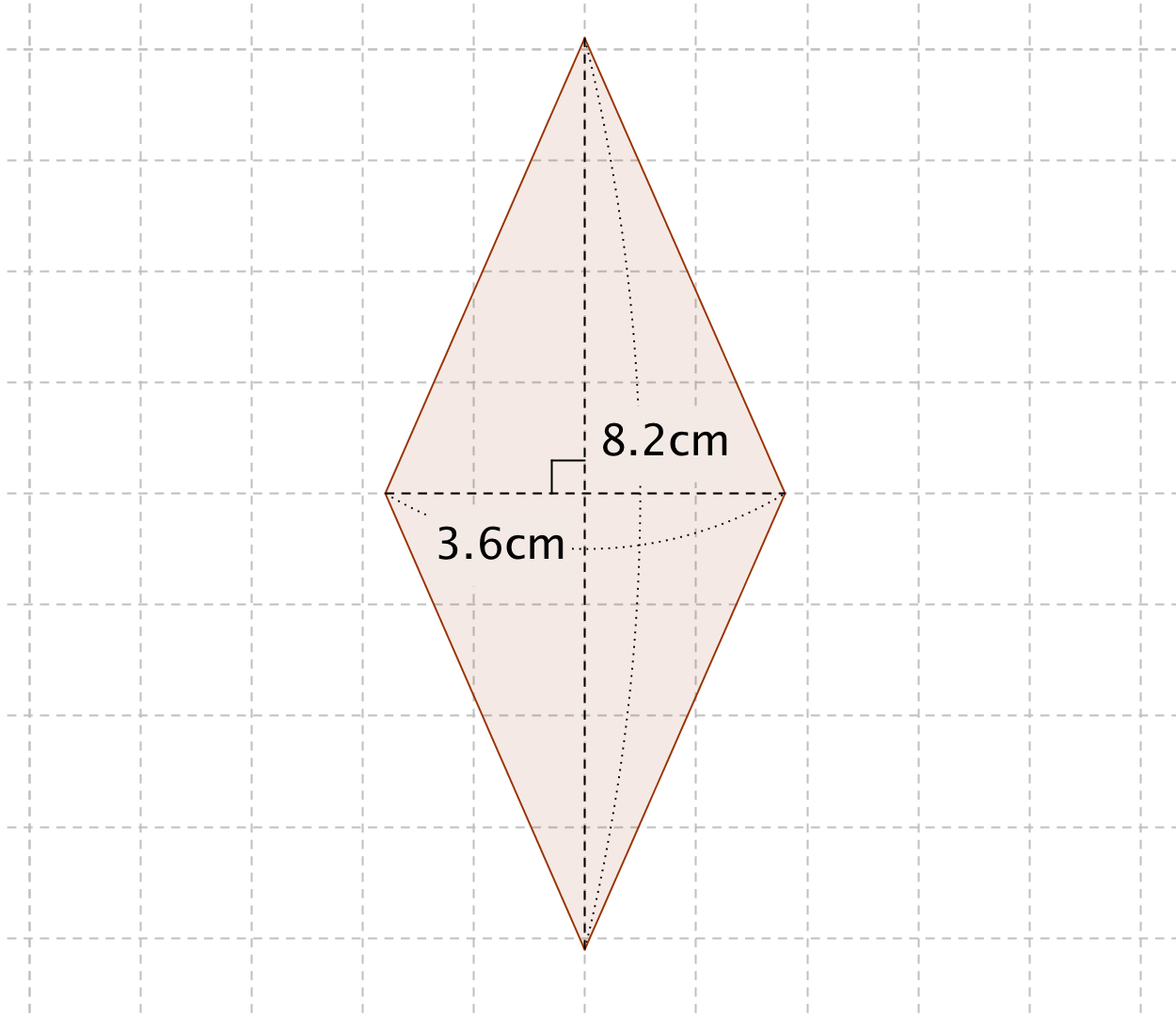



ひし形の面積の公式 算数の公式
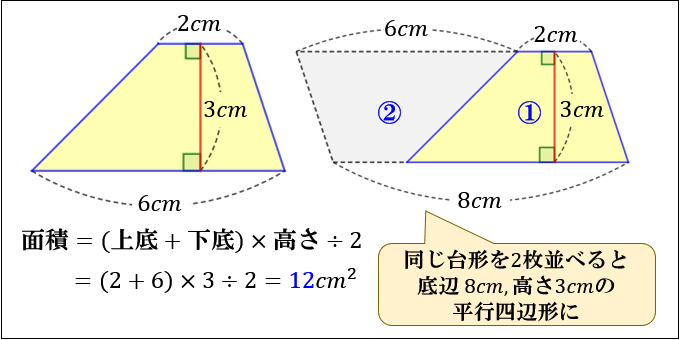



四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ



3
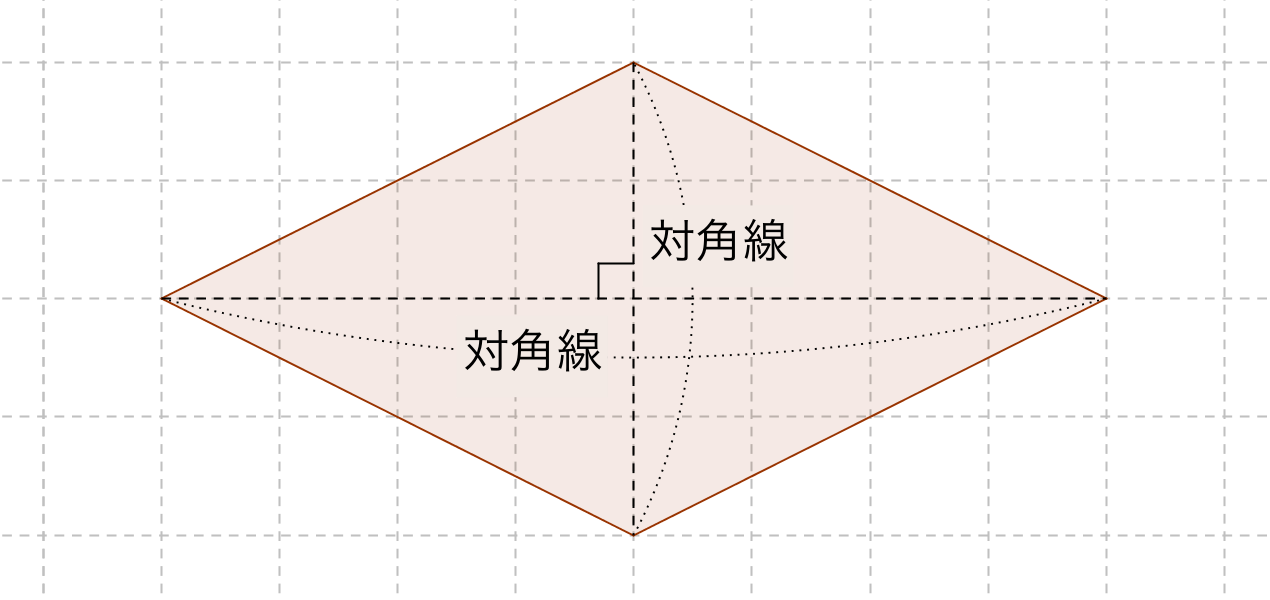



ひし形の面積の公式 算数の公式




菱形 Wikipedia
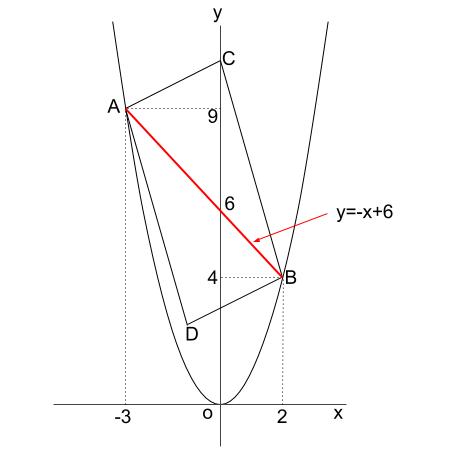



2乗に比例 平行四辺形の面積 中学数学の無料オンライン学習サイトchu Su




平行四辺形の対角線の長さの求め方


